Предложен метод численного исследования влияния параметров элементов линейных электрических цепей в режиме переменного тока на режимы работы цепей, обеспечивающий предельно малые вычислительные затраты.

При изучении термодинамических процессов, протекающих в пористой среде с газовым гидратом, в зависимости от состава фаз выделяют три зоны: гидратно-талую, где присутствует H2O и газ без гидрата, гидратно-равновесная – H2O, газ и гидрат, гидратно-стабильная зона – гидрат и H2O или газ. В данной работе используется модель фазово-термодинамических определителей для перехода между зонами. 

Работа посвящена решению задачи о распаде произвольного разрыва с использованием полностью консервативных разностных схем с адаптивным искусственным вязким наполнением. В исследовании рассматривается разностная схема, обеспечивающая выполнение закона сохранения в численном моделировании течений сжимаемого газа в эйлеровых переменных. Применённый метод протестирован на классической задаче Сода, и результаты вычислений показали хорошее соответствие с аналитическим решением.

В данной работе исследованы методы добавления адаптивной искусственной вязкости для полностью консервативных разностных схем в переменных Эйлера. С помощью предложенных методов проведены расчёты тестирования в задаче о распространении двух симметричных волн разрежения в противоположные стороны (задача Эйнфельдта). Расчеты демонстрируют очень хорошее совпадение численного и аналитического решений классической задачи Эйнфельдта.

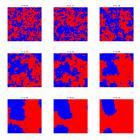
В данной работе исследуется взаимосвязь между статистической механикой спиновых стекол и обучением нейронных сетей с использованием многослойной модели Шеррингтона–Киркпатрика для анализа энергетических ландшафтов и фазовых переходов. Численное решение уравнений Thouless-Anderson-Palmer, использующее стохастический градиентный спуск с моментом, демонстрирует аналогию между переходом физической системы в состояние порядка и стабилизацией весов нейросети.

В работе разрабатывается новая версия компилятора для DVM-системы, которая использует подход OpenMP Offload для эффективного выполнения программ на различных вычислительных ускорителях (например, GPU и CPU). 

В предлагаемом докладе рассмотрена задача оптимального граничного управления некоторой распределенной неоднородной колебательной системой, состоящей из двух разнородных участков, которая описывается одномерным волновым уравнением, характеризующим продольные колебания неоднородного стержня или поперечные колебания неоднородной струны с заданными начальным и конечным условиями.

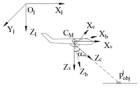
В данной работе, на основе полученных данных из видеокамеры прикреплённой к БПЛА, с учетом закона движения, предлагается математическая модель, описывающая координатно-временную зависимость БПЛА и движущейся цели. Используя указаную математическую зависимость двух объектов, в частности, можно разрабатывать алгоритм управления БПЛА, обеспечивающий сближение с подвижной целью.

В работе исследованы три различных подхода к адаптации шага по времени в модели развития канала электрического пробоя типа диффузной границы. Один из подходов предложен авторами настоящей работы, дано его теоретическое обоснование. Для всех трех алгоритмов адаптации проведены численные эксперименты; выявлен наиболее эффективный из них.

Исследованные алгоритмы адаптации универсальны – они могут использоваться и в других моделях типа диффузной границы с уравнением Аллена–Кана.

Как хорошо вы знаете правила и законы математики? Возможно, вы в совершенстве разбираетесь во всех областях этой удивительной, крайне влиятельной, а главное, интересной науки. Если я вам скажу, что в математике, помимо обычных задач существуют ещё и нестандартные задачи, которые не поддаются обычным законам математики. Заинтересовала? Не сомневаюсь. Такие задачи поподаютсяабсолютно всем школьникам, но не все их умеют решать. 

Термодинамические функции и уравнения, описывающие ту или иную систему, не являются независимыми. Применение уравнений состояний, которые  не согласованы с другими функциями задачи при теоретическом анализе или численном моделировании может привести к неверным результатам: нефизическим решениям или численным  неустойчивостям на счете. Выполненное в работе согласование функций и уравнения состояния значительно повышает надежность расчета фазового равновесия нефти и газа.

Работа посвящена изучению взаимодействия металлических нанокластеров

Исследование распределения размеров клеток и их корреляции с числом соседей в моделях эпителиальной ткани с использованием методов оптимизации упаковки частиц

Числа Фибоначчи привлекали внимание и вдохновляли математиков ранее и вызывают интерес у современных ученых, они являются связующим звеном окружающего мира. Изучение чисел Фибоначчи в рамках программы школы носит ознакомительный характер, однако их распрстраненность в окружающем мире диктует необходимость более пристального их рассмотрения.

При применении классического разрывного метода Галеркина для численного решения задач газовой динамики, возникает необходимость использования минимаксных процедур коррекции численных потоков или лимитеров для сохранения монотонности решения. Применение таких лимитеров может повлиять на точность полученного решения, понижая ее. В качестве альтернативы применения процедуры лимитирования, в данной работе, используются базисные функции, зависящие от времени.

Есть задача дискретной оптимизации. Сведение этой задачи к модели Изинга, для примерного нахождения решения.