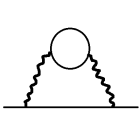
В данной работе мы, в рамках скалярной квантовой электродинамики на фоне продолжительного электрического пульса, рассматриваем одно- и двухпетлевые поправки к электрическому току, выделяя вклады, растущие по продолжительности пульса. Лидирующие петлевые интегралы мы оцениваем в пределе слабого внешнего поля, используя WKB-приближение, с целью понять, при каких значениях продолжительности пульса соответствующая поправка к току станет сравнимой с древесным результатом для швингеровского тока.

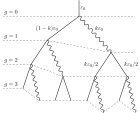
Рассматривается обобщение модели Гайтлера в применении к электромагнитному каскаду в постоянном скрещенном поле. Получена оценка для финального числа лептонов в пределе большого значения квантового параметра затравочного электрона (позитрона).

В данной работе показано, как когомологическая техника может быть применена при построении инвариантных функционалов в теории высших спинов. В задаче рассматривается расширенная система нелинейных уравнений Васильева.

В нашей работе мы явно вычислили все вершины взаимодействия симметричных калибровочных полей высших спинов вне массовой оболочки в локальной форме. 
Дополнительно было показано, что вершины имеют вид интегралов по фазовому пространству, которое удобно представлять как пространство многоугольников специального вида.

В работе рассматриваются три-векторные деформации Янга–Бакстера различных десятимерных фонов и анализируется динамика двумерных сигма-моделей над ними. Изучается классическое фазовое пространство данной системы, в частности, поведение КАМ-торов и Ляпуновской экспоненты при различных параметрах деформации. Полученные результаты согласуются с аналитическими, а также служат мотивацией к будущему исследованию моделей, фазовые траектории которых демонстрируют поведение интегрируемой системы.

В данной работе проиллюстрирован квантовый эффект Зенона. Предложена схема для анализа влияния одного квантового состояния кубита на квантовое состояние другого кубита. 

В данной работе рассматривается теория фотоэлектронного циркулярного дихроизма. Получено  точное выражение для коэффициента $${{b}_{1}}^{\{+1\}}$$, характеризующего асимметрию углового распределения фотоэлектронов в хиральных молекулах, через матричные элементы дипольного момента.

В случае нарушения аксиальной симметрии плазменного «пузырька» меняется конфигурация полей внутри полости, что приводит к возникновению сильных поперечных полей и возникновению неустойчивостей. Работа основывается на модификации недавно полученной модели на случай источника с эллиптичностью. Удалось получить точное аналитическое выражение с учетом эллиптичности «пузыря» в зависимости от продольной координаты и радиуса недеформированной полости. 

 Одной из модификаций общей теории относительности является симметричная телепараллельная теория относительности. В таком формализме мы изучаем свойства вакуумных уравнений движения в линейном приближении  в плоском пространстве Минковского. Применяя методы теории возмущений, мы получаем систему линейных уравнений, из которой мы устанавливаем, какие степени свободы являются динамическими, какие калибровочными, а какие ограничены ограничениями.

В работе исследуется эволюция масс и других наблюдаемых типа массы/радиуса Чандрасекара и абсолютной светимости сверхновых типа Ia в рамках конформной модификации стандартной космологии. Выясняется природа расхождения между предсказаниями фотометрических расстояний в этих моделях.

В данной работе мы обобщаем неравновесную диаграммную технику Келдыша на случай негауссовых начальных состояний.

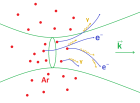
Рассматривается туннельная ионизация атомарного аргона в фемтосекундном лазерном импульсе с интенсивностью близкой к 10^22 Вт/см2 с целью исследования релятивистской динамики и излучения фотоэлектронов, высвобождаемых из ионов в лазерном фокусе. Излучение электронов усиливается при столкновении с встречным лазерным импульсом. Показано, что угловые распределения и спектры испускаемых фотонов могут служить инструментом для определения пиковой интенсивности основного импульса в фокусе. 

В работе рассматриваются взаимодействия струн на уровне дерева. Изучаются их аналитические свойства, а именно каким они могут удовлетворять уравнениям. Особый акцент сделан на анализе предела Редже.

Метод экспериментального определения эвтектики давно и широко применятся для систем с относительно низкой температурой плавления, однако большинство современных перспективных соединений являются тугоплавкими с температурой плавления выше 3000 К, что делает экспериментальный поиск эвтектики в таких системах дорогостоящим и сложным. Мы попытались облегчить эту задачу. Для этого был предложен метод определения эвтектики с помощью моделирования тугоплавких соединений нейросетевым потенциалом.

В данной работе делаются обобщения TsT-деформаций в контексте три-векторной и выявлен характер некоторых наблюдаемых особым образом деформированной модели ABJM.

Я расскажу про два способа построения минимальных онородных дифференциальных уравнений по одной переменной с рациональными коэффициентами на петлевыве Фейнмановские диаграммы в координатном и импульсном пространстве. Также расскажу про особенности их связи при помощи преобразования Фурье.

Данный доклад посвящён обзору результатов обобщения бивекторных деформаций супергравитации типа IIB до четырёхвекторных и сравнению голографических картин в бивекторном и обобщенном случаях.

В работе произведён анализ диаграмм трёхфотонного обмена в рамках формализма двухвременной функции Грина в картине Фарри. Был разработан программный пакет, проводящий вывод аналитических выражений вкладов в энергию для всех диаграмм N-фотонного обмена. Полученные выражения сверены с ручным выводом до N = 3. Для диаграмм трёхфотонного обмена получено брейтовское приближение. Исследован вопрос сокращения инфракрасных расходимостей, рассмотрены методы их выделения для диаграмм высокого порядка.

Ранее в голоморфном секторе теории высших спинов был найден нетривиальный вакуум, содержащий скалярные поля. Этот вакуум является кандидатом на описание спонтанно нарушенной симметрии HS в трёх измерениях. Работа посвящена изучению этого вопроса

В докладе обсудим, как с помощью матриц Гёрица, отражающих топологию узлов, вычислять скобки Кауффмана и, как следствие, полиномы Джонса только от изначального вида диаграммы узла. Покажем пути обобщения этого метода на полиномы ХОМФЛИ-ПТ, которые являются обобщением полиномов Джонса и корреляторами от вильсоновских петель в теории Черна-Саймонса для калибровочной SU(N) при произвольном N.

В работе исследуется движение точечной частицы на фоне киральной теории высших спинов. Действие анализируется в рамках теории возмущений по количеству полей высших в вершине взаимодействия , с акцентом на втором порядке. Основной результат работы заключается в том, что нетривиальное взаимодействие между точечной частицей и полями высших спинов отсутствует.

В докладе представлена методика определения уровня k в теории Черна–Саймонса с группой SU(2), использующая анионы – частицы, возникающие при взаимодействии частиц с полем Черна–Саймонса. Авторы основываются на идее переплетения мировых линий трёх анионов в 2+1 мерном пространстве-времени и измерении вероятности аннигиляции пары, зависящей от параметра k. Подробно описываются необходимые для этого эксперимента операции и их порядок.

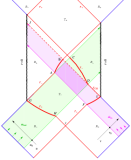
В настоящей работе мы обобщаем понятие моста Эйнштейна-Розена, определяя его как пространственно-подобную связь между двумя вселенными с асимптотически минковскими областями пространства-времени в пределе больших расстояний от горизонтов. Так же рассматривается возможные способы решения проблемы инфляции в метрике Рейсснера-Нордстрема.

В работе исследуются решения линеаризованных уравнений Васильева для трёхмерной теории высших спинов с помощью нового метода дифференциальных гомотопий. Показано, как с помощью этой техники описать все решения, не перепутывающие динамические и топологические поля. В частности, воспроизведены все полученные ранее другими методами решения.

В работе рассматриваются легкие скалярные частицы в  пространстве де-Ситтера с самодействием фи в кубе. Получены ассимптотические решения уравнения Дайсона в EPP и CPP

Для КТП на решётке размерностью d⩾3 энергия вакуума (как бозонного, так и
фермионного) равняется нулю, если гамильтонианом является функция от квадрата импульса, а вычисление энергии вакуума ведётся в кольце остатков по модулю N. Данный факт связан задачей из теории чисел о числе способов разбиения числа на сумму N квадратов в кольце остатков по модулю N. В докладе исследуется формула для кратности, полученная для случая N, равного степени простого числа.

В данной работе вычислена КЭД поправка к энергии основного состояния связанного электрона, соответствующая диаграмме собственной энергии. Показано, что использование калибровки Кулона позволяет существенно повысить точность расчетов по сравнению с калибровкой Фейнмана.

В работе исследуется эволюция со временем метрики чёрной дыры Шварцшильда - де Ситтера в модифицированной теории гравитации, представляющей собой модель к-эссенции. Найдены явные формулы для зависимости масштабного фактора и видимых горизонтов чёрной дыры от времени. Также в данной теории исследованы возмущения определённого вида и получены поправки к метрике в соответствии с ними.

Все знают, что теория дифференциальных форм степени 1 и их контурных интегралов допускает неабелево обобщение -- получается теория связностей и упорядоченных интегралов. Я расскажу про подход к построению аналогичной теории для старших форм, который мне кажется перспективным. Подход, о котором идёт речь, подразумевает вывод следствий типа Стокса для нелинейных дифференциальных уравнений; я расскажу, чего на этом поле мне удалось добиться и что ещё предстоит сделать.

В работе получено эффективное действие для Г-подсистемы Изинговского сверхпроводника, учитывающее симметрию системы, синглетное и триплетное взаимодействия. Причём для обеспечения калибровочной инвариантности необходимо вводить в триплетное взаимодействие члены зависящие от вектор-потенциала A. Действие обобщает использованные ранее модели, поскольку взаимодействие в нём локально в пространстве, что позволяет рассматривать не только однородные системы. 

В работе при помощи когомологической техники развернутого формализма получена полная классификация билинейных сохраняющихся токов высших спинов в 4d теории. Установлено соответствие между данными токами и известными кубическими вершинами, при этом показано, что в некоторых случаях вершины содержат дополнительные члены со старшими производными, как было известно ранее для вершины Васильева-Фрадкина. Также показано, что все найденные токи являются бесследовыми.

В работе рассматривается электрический заряд, равномерно ускоряющийся вдоль направления x и движущийся с постоянной скоростью вдоль направления y. Мы показываем, что в соускоряющейся вдоль направления x системе отсчета Риндера этот заряд создает ненулевой вектор Пойнтинга, что, однако, не приводит к неисчезающему потоку через бесконечно удаленную поверхность. Кроме того, мы показываем, что в лабораторной системе отсчета Минковского такой заряд создает поток, который не исчезает на бесконечности.

В данной работе изучается временная эволюция скалярного квантового поля в результате локального квантового квенча (быстрой смены параметров) в квазиклассическом приближении в технике Келдыша. 

После 100 лет попыток описать квантовую систему функцией распределения вероятности эта задача, наконец, решена.

А именно, найдена формула для обратимого отображения волновой функции квантового состояния на соответствующее ему распределение вероятности.

Введённое вероятностное представление квантовых состояний находится в согласии с соотношением неопределённостей Гейзенберга и удовлетворяет новому статистическому уравнению, эквивалентному уравнению Шрёдингера для волновой функции.