In this text we consider random operators on some Banach space X. The law of large numbers is obtained in another work for X being the space of sequences. In this work we obtain the law of large numbers for the case when X is the space of linear operators on the Banach space of Schatten-class operators.

Получен критерий Z_2-вложимости джойностепени в 2k-мерные многообразия:

С использованием представления Крауса для параметризации квантовых каналов точками факторизованного комплексного многообразия Штифеля устанавливается гомеоморфизм этого фактора и топологического пространства квантовых каналов. Это позволяет проанализировать точки экстремума функционалов на многообразиях Штифеля, важных для квантовой теории. Также доказывается, что метрика, индуцированная римановой метрикой на комплексном многообразии Штифеля, является обобщением угла Бюреса для матриц плотности.

Будет обсуждаться вопрос аппроксимации bi-непрерывной полугруппы T(t) итерациями Чернова

F(t/n)^n ≈ T(t)

в более слабых предположениях, чем в исходной теореме Чернова (которая непосредственно используется при доказательстве).

Класс bi-непрерывных полугрупп обобщает класс сильно непрерывных полугрупп, и все результаты можно понимать для последних.

Результаты могут быть непосредственно применены в вопросах квантовых случайных процессов.

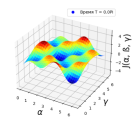
В работе исследуются свойства функционала максимизации среднего квантовой наблюдаемой для замкнутой квантовой системы в случае управления одним кубитом. Рассматриваются управления вида "импульс-ожидание-импульс". Для некоторых систем, для которых ранее не было исследовано существование или отсутствие ловушек (точек локального, но не глобального экстремума целевого функционала), доказано отсутствие ловушек при малых временах.

В данной исследовательской работе рассматривается статья М.Д. Юдина, словесные формулировки из данной статьи расписываются в аналитическом виде

Работа посвящена проблеме локальной диагонализуемости пары квадратичных дифференциальных форм от двух действительных переменных. Эта задача естественным образом обобщает аналогичную для алгебраических квадратичных форм. В случае дифференциальных форм возникает дополнительное препятствие к диагонализации, связанное с диагонализацией вырожденных квадратичных форм, имеющих в исследуемой точке нулевые коэффициенты (омбилическая точка).

Доказаны достаточные условия C0- Ω-взрыва в C1-гладких простейших (то есть имеющих ограниченное множество наименьших периодов периодических точек) косых произведениях на многомерных клетках и приведены примеры реализации этих условий.

Из теоремы Сарда следует, что для функций $$f:[0,1]^{2}\to \mathrm{ℝ}$$ класса $${C}^{2}$$ образ под действием $$f$$ меры Лебега, суженой на критическое множество $$f$$, взаимно сингулярен с мерой Лебега на $$\mathrm{ℝ}$$. Мы показали, что для функций класса $${C}^{1,\alpha }$$ с $$0<\alpha <1$$ это свойство сильнее слабого свойства Сарда, введённого Альберти, Бьянкини и Криппа.

В работе обсуждается возможность обобщения результатов работ [Reich D. M.[et al.] Phys. Rev. A 2013 V.88:042309; Goerz M. H. [et al.] New J. Phys. 2014 V.16:055012] о минимальном количестве квантовых состояний, необходимых для определения унитарного квантового канала, на случай бесконечномерного сепарабельного гильбертова пространства. Кроме того, рассматривается вопрос о минимальном количестве квантовых состояний, необходимых для определения некоторых не унитарных квантовых каналов.

Изучена структура омега-предельных множеств простейших косых произведений с фазовым пространством в виде клетки произвольной размерности n>2. Найдены необходимые условия существования одномерного омега-предельного множества у отображений рассматриваемого типа. Построен пример отображения, имеющего одномерное омега-предельное множество.

В работе приведено построение комплексного представления тройного накрытия группы A6 в наименьшей возможной размерности. Помимо этого, получена конструкция тройного накрытия группы Aut A6, а также доказана вложимость A6 в L_3(4) и M10 в U_3(5).

В работе рассматривается задача восстановления контуров, или очертаний, объектов, находящихся в поле зрения. Д. Мамфордом был предложен метод решения данной задачи для плоского изображения, основанный на оптимизации функционала эластики, называемый в работе функционалом Мамфорда-Эйлера. Целью настоящей работы служит обобщение плоского случая на сферу, что позволяет включить в рассмотрение также геометрические модели человеческого зрения.