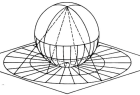
В работе описаны спектральные серии оператора Лапласа — Бельтрами на двумерной сфере, причем метрика на ней поднимается из стандартной метрики Фубини-Штуди на CP¹ при помощи двулистного накрытия.

Мы разрабатываем метод построения глобальной асимптотики для решений разностных уравнений на основе квазиклассического приближения. Идея состоит в сведении разностного уравнения к псевдодифференциальному и применении канонического оператора Маслова [1], связанного с геометрическим объектом в фазовом пространстве — лагранжевым многообразием.

В докладе мы проиллюстрируем развиваемый подход на примере полиномов Якоби, для которых возникает асимптотика через функцию Бесселя

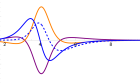
Набег длинных волн на берег описывается системой мелкой воды, асимптотики которой легко строятся по решению линеаризованной системы, эквивалентной волновому уравнению с вырождающейся скоростью, причем точка вырождения соответствует берегу.  В докладе разбирается влияние на отражение волны типа граничных условий в точке вырождения: Дирихле, Неймана и Робена и условия ограниченности интеграла энергии.

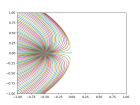
В работе А.Ю. Аникина, С.Ю. Доброхотова, В.Е. Назайкинского, М. Руло описан алгоритм построения асимптотического решения псевдодифференциальных уравнений с локализованной правой частью в виде канонического оператора на лагранжевом многообразии состоящем из траекторий системы Гамильтона, выпущенных из точки источника. Основным условием для применения этого алгоритма является покидание траекториями любой конечной области за конечное время. Рассмотрим примеры, когда это условие не выполняется.

1. В докладе представлены асимптотические решения нелинейной системы уравнений мелкой воды с ровным наклонным дном, соответствующие береговым волнам, бегущим вдоль береговой линии. Асимптотические решения системы нелинейных уравнений мелкой воды записаны в виде параметрически заданных функций, определяемых через точные решения линеаризованной системы. 

 Работа выполнена в рамках гранта РНФ №24-11-00213.

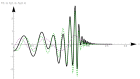
Волны на поверхности жидкости над неровным дном в поле описываются уравнением с псевдодифференциальным оператором,который учитывает эффект дисперсии.В данной работе рассматривается одномерный случай и ставится задача Коши с локализованным начальным условием и краевым условием непротекания на жесткой вертикальной стенке.В работе исследуется отражение волны от стенки и влияние дисперсии на начальное возмущение.Асимптотики задачи строятся в виде канонического оператора Маслова с граничным индексом.

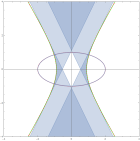
В докладе будет приведена параметризация для соответствующего лагранжева многообразия и изучен случай с каустикой в виде гиперболы. В частности, мы приведем глобальные асимптотики для собственных функций оператора Лапласа в терминах функции Эйри и получим условие квантования на границу области с фиксированной каустикой.

Доклад основан на совместной работе с А.В. Цветковой.

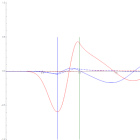
Нами рассматривается неоднородное волновое уравнение для круглого диска с прозрачной стенкой, где ставятся условия непрерывности функции и ее нормальной производной. Правая часть представляет собой точечный источник, гармонический по времени. Мы исследуем зависимость параметров решения от положения и частоты источника, в том числе взаимосвязь с квазистационарными состояниями, соответствующими рассматриваемому диску с прозрачными стенками.

В работе изучается волновое уравнение, скорость которого имеет локализованное возмущение в некоторой точке $x_0$. Начальное условие имеет вид быстроосциллирующего волнового пакета, длина волны которого не сравнима с масштабом неоднородности. В данном случае длина начальной волны порядка $\varepsilon,$ а ширина локализованной неоднородности порядка $\sqrt{\varepsilon},$ где $\varepsilon$ -- малый параметр, который стремится к 0.

Точечный процесс с гипергеометрическим ядром был получен Бородиным и Ольшанским как спектральное разложение мер Хуа-Пикрелла на бесконечных эрмитовых матрицах с действием бесконечной унитарной группы: эргодические меры в этой конструкции параметризуются счетными дискретными подмножествами прямой. Для произвольной функции исследуются ее аддитивные функционалы - сумма функции в точках случайного подмножества. В работе показано, что при растяжении функции эти величины сходятся к гауссовским.

В работе исследован алгоритм быстрого обратного преобразования Лапласа. Написан и улучшен алгоритм, переводящий функции из области изображений в область оригиналов. Изучен эксперимент по загрузке мирамистина в частицы SiO2. Он описан уравнениями, решенными в области изображений. С помощью программы решение было получено в области оригиналов. Получилось хорошее согласие расчета с экспериментом. Этот подход - основа для исследования взаимодействия с окружающей средой лекарственных препаратов.

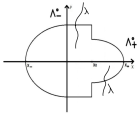
Построены квазиклассические спектральные серии одномерного оператора Шрёдингера с потенциалом, испытывающим резкий скачок вблизи фиксированной точки. В данном докладе будет рассмотрен случай, когда ширина скачка много больше длины волны де Бройля. Асимптотика строилась с помощью метода канонического оператора Маслова.

Работа посвящена квазиклассическим асимптотикам уравнения Шредингера с дельта-потенциалом. Область определения таких операторов требует от решения выполнения определенных краевых условий в точках носителя дельта-особенности. Описывается перестройка геометрических объектов, отвечающих решению, при взаимодействии с дельта-потенциалом.